いきなりOpenFOAM (20)
ジューコフスキー翼周りの解析(ポテンシャル流れ解析)
解析の手順
前回は、回転する円柱周りの流れを解析しました。この結果に適当な座標変換を施すと、翼周りの流れを求めることができます。今回は、ジューコフスキー翼の揚力係数と翼周りの流線をポテンシャル流れ解析で求めてみます。
手順としては、始めに中心が原点からずれた単位円を描きます。単位円に適当な循環を与えて、ポテンシャル流れ解析を行い、流線を求めます。単位円および得られた流線にジューコフスキー変換を施すと、ジューコフスキー翼と翼周りの流線が得られます。
ジューコフスキー変換
詳細な説明は割愛しますが、座標系の格子の辺のなす角度が変換前後で等しくなるような変換を等角写像と呼び、ポテンシャル流れは等角写像を行っても成り立ちます。つまり、ある座標系でポテンシャル流れ解析を行い、流線が得られたら、等角写像で座標を変換すると、その座標系での流線が得られます。
ジューコフスキー変換は単位円を翼型に変換する等角写像の一種で、下記の式で表されます。
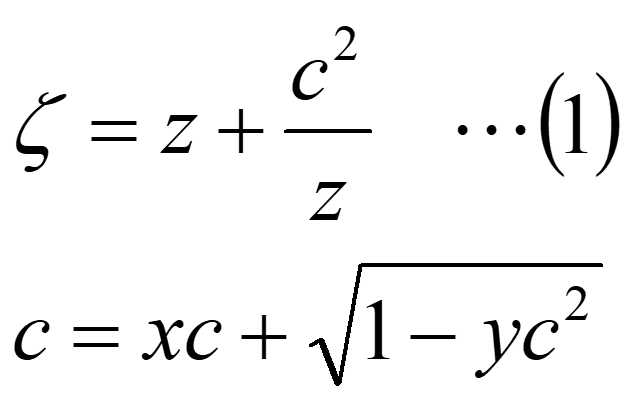
ここで、zは座標の複素表示でz=x+i*yで、xcおよびycは単位円の中心座標です。
原点から中心がずれた単位円を(1)式で変換し、得られたζの実部と虚部をプロットすると、ジューコフスキー翼が描けます。以上の操作を行うPythonコードを下記に記します。
import numpy
from matplotlib import pyplot
pi=numpy.pi
xc=-0.1
yc=0.1
a=10
a=numpy.deg2rad(a)
z=numpy.exp(1j*numpy.linspace(0,2,100)*pi)+xc+1j*ycc=xc+numpy.sqrt(1-yc**2)zeta=lambda z:(z+c**2/z)*numpy.exp(-1j*a)
pyplot.plot(z.real,z.imag)
pyplot.plot(zeta(z).real,zeta(z).imag)
pyplot.grid('on')
pyplot.xlim([-2,2])
pyplot.ylim([-2,2])
pyplot.gca().set_aspect('equal')
pyplot.show()
x=zeta(z).real
y=zeta(z).imag
上記コードの4行目、5行目のxc、ycが単位円の中心座標で、xcを小さくすると(負の値なので絶対値は大きく)翼の厚みが増加します。また、ycを増加させると翼の反りが増加します。6行目のaは迎角で流れに対して翼が成す角度です。迎角aの単位はこのコードでは度にしています。8行目で単位円を変数zとして作成し、10行目ではラムダ関数で変数zetaにジューコフスキー変換を設定しています。なお、10行目のラムダ関数には迎角a分の座標回転も入れています。zeta(z)とすると、ジューコフスキー変換が施された単位円が求められます。11行目以降で、zとzetaをプロットしています。
以上のコードを動作させると、図1に示すような単位円とジューコフスキー翼形状が得られます。xcとycを変えると、ジューコフスキー翼の形状も変化します。
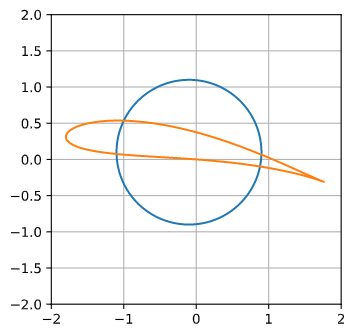
翼周りの流線を表示
次に円柱周りの流線を表示させるコードは、第18回と基本的に同じですが、翼の後端で流れが合流するような循環を与えることがポイントになります。これをクッタの条件と呼びます。
クッタの条件を満足する循環はジューコフスキー翼では下記の式で求められます。
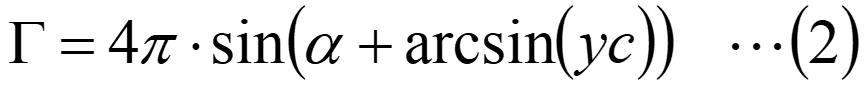
ここで、αは迎角[rad]、ycは単位円の中心y座標です。揚力係数CLは、第18回で説明したように、単位円では循環と等しくなるため、下記の式で求められます。
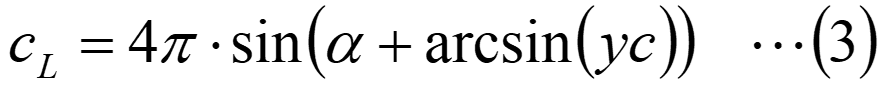
等角写像の性質から、ジューコフスキー変換を施した翼形状に対しても(3)式は成り立つため、ジューコフスキー翼の揚力係数は(3)式で求めることができます。(3)式を見ると、迎角αを増加させたり、翼の反りを増加させたりすると、揚力係数が増加することがわかります。実際の翼では失速するため、迎角や反りを大きくするとある値以上では揚力係数が減少しますが、(3)式は理想流体を基にした結果のため、失速については計算できません。また、第19回で見たように、実際の回転する円柱と周囲流体との間にはすべりがあるため、揚力係数は循環から求めた揚力係数よりも小さくなります。ジューコフスキー翼についても同様で、揚力係数は(3)式で求めた値よりも小さくなります。これは次回、OpenFOAMで解析して、(3)式による結果と比較してみます。
クッタの条件を満足する循環を与えられた円柱周りの流線を表示するPythonコードを下記に記します。3行目が反りに相当する単位円の中心y座標yc、4行目が迎角a[度]です。下記のコードを実行すると、図2に示すような円柱周りの流線が得られます。
import numpy
from matplotlib import pyplot
yc=0.1
a=10
a=numpy.deg2rad(a)
pi=numpy.pi
G=4*pi*numpy.sin(a+numpy.arcsin(yc))
xy=numpy.arange(-3,3,0.01)
(x,y)=numpy.meshgrid(xy,xy)
z=x+1j*yW=(z*numpy.exp(-1j*a)+1/z*numpy.exp(1j*a))+1j*G/2/pinumpy.log(z)psi=W.imagpsi=numpy.where(numpy.abs(z)<=1,0,psi) pyplot.contour(x,y,psi,levels=numpy.arange(-4,4,0.2)) zz=numpy.exp(1j*numpy.linspace(0,2,100)*pi)
pyplot.plot(zz.real,zz.imag)
pyplot.gca().set_aspect('equal')
pyplot.show()

以上をまとめると、ジューコフスキー翼周りの流線を表示できます。下記にそのPythonコードを記します。動作させた結果は図3のようになります。翼端で流れが合流し、クッタの条件を満足していることがわかります。また、翼上面側の流線間隔は、翼下面側よりも狭くなっていて、流速が増加していることがわかります。ベルヌイの定理から翼上面では静圧が低下し、翼下面では静圧が上昇することで揚力が発生することがわかります。この場合の揚力係数は(3)式から、Cl=3.4となります。
import numpy
from matplotlib import pyplot
pi=numpy.pi
xc=-0.1
yc=0.1
zc=xc+1j*yca=10a=numpy.deg2rad(a)G=4*pi*numpy.sin(a+numpy.arcsin(yc))c=xc+numpy.sqrt(1-yc**2)zeta=lambda z:(z+c**2/z)*numpy.exp(-1j*a)xy=numpy.arange(-4,4,0.01)(x,y)=numpy.meshgrid(xy,xy)z=x+1j*y
W=(z*numpy.exp(-1j*a)+1/z*numpy.exp(1j*a))+1j*G/2/pi*numpy.log(z)
psi=W.imag
psi=numpy.where(numpy.abs(z)<=1,0,psi)
pyplot.contour(zeta(z+zc).real,zeta(z+zc).imag,psi,levels=numpy.arange(-4,4,0.2))
zz=numpy.exp(1j*numpy.linspace(0,2,100)*pi)+zc
pyplot.plot(zeta(zz).real,zeta(zz).imag)
pyplot.xlim([-3,3])
pyplot.ylim([-3,3])
pyplot.gca().set_aspect('equal')
pyplot.show()

なお、クッタの条件を満足しないとどうなるのかを上記のコードで9行目の式をG=0として計算してみると、図4に示すように、翼端を流れが回り込むという現実にはあり得ない状況となります。つまり、クッタの条件を満足しないと計算結果は現実にはあり得ない状況となります。言い方を変えると、クッタの条件を満足する循環を与えることで、その循環により翼に揚力が発生するというメカニズムになります。ちょっとトリッキーな説明のように見えますが、その後の実験や解析により、翼には循環が発生していることが確認されています。翼周りに発生する循環は次回、確認してみます。

今回はジューコフスキー翼周りの流れをポテンシャル流れの例で紹介しました。
次回は、ジューコフスキー翼のモデルを作成し、OpenFOAMで流線と揚力係数を求めてみます。あわせて、翼周りに循環が発生しているのか確認してみます。
おことわり
本コンテンツの動作や表示はお使いのバージョンにより異なる場合があります。
本コンテンツの動作ならびに設定項目等に関する個別の情報提供およびサポートはできかねますので、あらかじめご了承ください。
本コンテンツは動作および結果の保証をするものではありません。ご利用に際してはご自身の判断でお使いいただきますよう、お願いいたします。

