いきなりOpenFOAM (84)
竹とんぼの飛行解析(その3)
竹とんぼの飛行高度を求める
前回(いきなりOpenFOAM第83回)で、下記(1)式と(2)式に示す竹とんぼの運動方程式の係数が、CADのプロパティやOpenFOAMによる数値風洞実験により求められました。
今回は、運動方程式を数値的に解いて、竹とんぼの高度の時間変化を求めてみます。
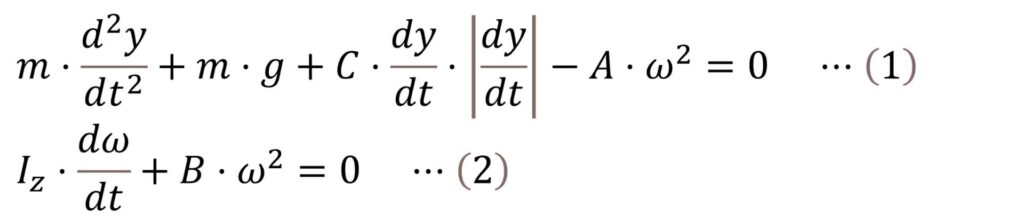
ここで、m=7.69×10-3kg、I=26.15×10-6kgm2、A=4.18×10-6N/(rad/s)2、B=0.17×10-6 Nm/(rad/s)2、C=4.87×10-3 N/(m/s)2で、yは高度[m]、tは時間[s]、ωは回転速度[rad/s]、gは重力加速度9.8m/s2です。
Pythonのソルバーodeintは1階微分への対応なので、(1)式と(2)式を下記のように、連立微分方程式に変更します。
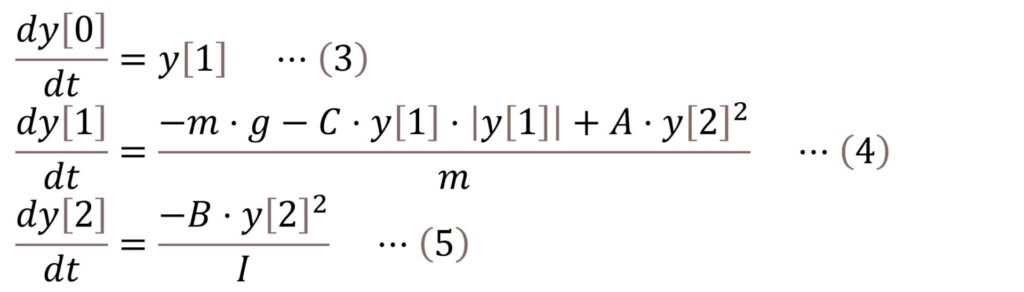
次に、yを配列変数として、lambda関数で(3)式、(4)式、(5)式を定義し、odeint関数で解くと、解が得られます。図1に具体的なコードを示します。詳細はいきなりOpenFOAM第60回を参照してください。

図1のコードを動作させると、図2に示すように、竹とんぼの高度の時間変化が得られます。図から、竹とんぼの最高高度は3.2mと求まります。
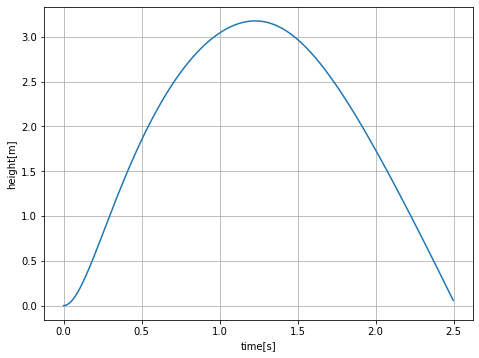
今回は運動方程式の係数A, B, Cの結果から、運動方程式を数値的に解いて、竹とんぼの高度の時間変化を求めました。
次回は翼断面形状が円弧翼の竹とんぼの飛行解析を行ってみます。
このページでは、各アプリケーションの操作説明は省略しています。FreeCADの具体的な操作については、いきなりOpenFOAM第5回および第7回、OpenFOAMでの計算実行は第8回、ParaViewの操作については第3回、第4回および第8回を参考にしてみてください。
おことわり
本コンテンツの動作や表示はお使いのバージョンにより異なる場合があります。
本コンテンツの動作ならびに設定項目等に関する個別の情報提供およびサポートはできかねますので、あらかじめご了承ください。
本コンテンツは動作および結果の保証をするものではありません。ご利用に際してはご自身の判断でお使いいただきますよう、お願いいたします。

