いきなりOpenFOAM (64)
インパルス応答解析の自動化(その1)
プログラムをセルに分割
前回までの説明で、振幅倍率の周波数特性は、インパルス応答波形から固有角周波数ωnと減衰比ζを求めることで、計算できることがわかりました。固有角周波数と減衰比はインパルス応答波形の隣り合った極大値から求められますが、任意の一か所の隣り合った極大値から求めるのではなく、全体の平均から求めると精度が良くなります。しかしながら、手作業で隣り合った極大値を探し出すのは手間がかかります。そこで、今回はバネマスダンパ系のインパルス応答波形から固有角周波数と減衰比を自動で求めるコードを作成してみます。
長くないコードなので、一気に全体を作成してもかまいませんが、セルに分割してコードを作成すると着実に作成できます。セルに分割して実行する仕組みはJupyterNotebookで行えますが、VisualStudioCodeでは、コードの行頭に#%%と入力することで、自動でセルに分割してくれます。
図1は、バネマスダンパ系のインパルス応答波形を計算するコードですが、先頭に#%%と入力すると、自動で、RunCell~が追加されます。「RunCell」をクリックすると、図1のコードが計算され、変数はすべてメモリ内に保存されます。したがって、先頭に#%%と記載して、図1の結果を処理するコードを作成すると、インパルス応答波形を変数t、yとして引き継いで計算することができます。これは、Pythonカーネルをリスタートしたり、VisualStudioCodeを終了したりしない限り、何度でも行えます。つまり、データ作成部分を作成して動作、データ処理部分を作成して動作、解析部分を作成して動作、結果表示部分を作成して動作といったように、機能ごとに分割してコードを作成することができ、コード作成のしきいを下げたり、デバッグを容易にしたりといった恩恵が得られます。また、numpyなどのモジュール類も有効であり、次のセルで再度、インポートする必要はありません。
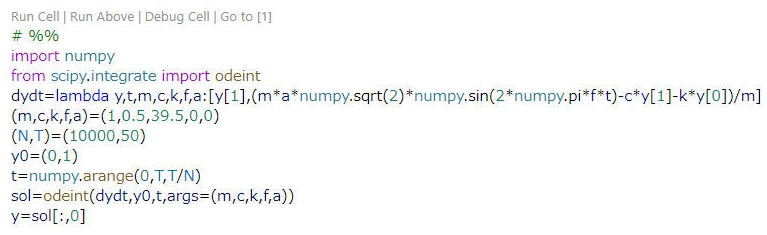
固有周波数の算出
次に、図1で計算したインパルス応答波形から固有周波数を求めてみます。固有周波数はインパルス波形をフーリエ解析し、スペクトルが最大となる周波数を求めることで得られます。離散フーリエ解析を行うため、from numpy import fftとして、fftモジュールをインポートします。なお、離散フーリエ解析はscipyモジュールでも行えます。fftモジュール内のfftfreq関数を使い、fftfreq(データ数、時間分解能)とすると、周波数軸を作成します。また、fft(データ)/データ数とすると、フーリエスペクトルが得られます。フーリエスペクトルは複素数であり、振幅を求めるには、絶対値を求めます(正しくは、複素共役との積の平方根ですが、絶対値absでも代用できます)。
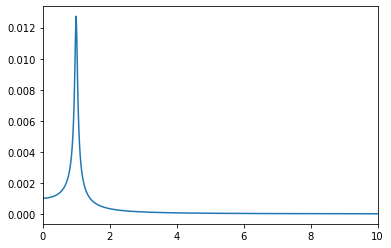
フーリエ解析では、サンプリング周波数を中心とした左右対称なスペクトルが得られるため、周波数、スペクトルともに[0:int(N/2)]として半分だけを使います。ちなみに、fftfreqで得られる周波数は0を中心とした周波数となるため、周波数0を中心とした左右対称なスペクトルとなります。図3は周波数と振幅とをプロットした結果です。1Hz付近にピークがあることがわかります。このピークのインデックスをargmaxで検出して、周波数を取り出すと固有周波数が得られます(MATLABなどでは関数maxでピーク値とインデックス双方が得られますが、numpyでは、関数maxでピーク値が、関数argmaxでピークのインデックスが得られます)。
ちなみにFFTとは高速フーリエ変換の略称で、データ数が2のべき乗以外では動作しませんが、FFT関数にはこの制約がありません。また、フーリエ解析では解析できる最大の周波数はサンプリング周波数の1/2となります(ナイキストの定理)。例えば、今回の例では、50秒を10000分割しているため、サンプリング周波数は200Hzであり、フーリエ解析では100Hzまでの成分が得られます。また、周波数分解能はサンプリング時間に反比例します。今回の例では、0.02Hzごとの成分が得られます。

減衰曲線の算出
次に、インパルス応答波形の極大値同士を結んだ曲線、すなわち減衰曲線を求めます。減衰曲線は、インパルス応答二乗積分あるいはシュレーダー積分で求められます。シュレーダー積分とはインパルス応答波形の瞬時値をp(t)とすると、下記の式で表される積分値です。
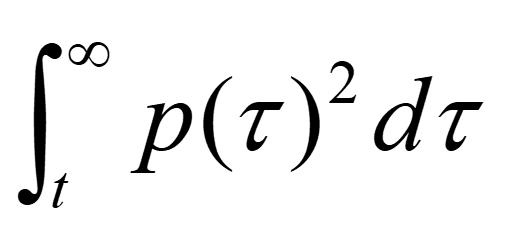
計算されたインパルス応答は離散値であることと、積分は瞬時値と時間刻みとの積の総和となることから、任意の時間tでの減衰曲線の値は下記の式で求められます。
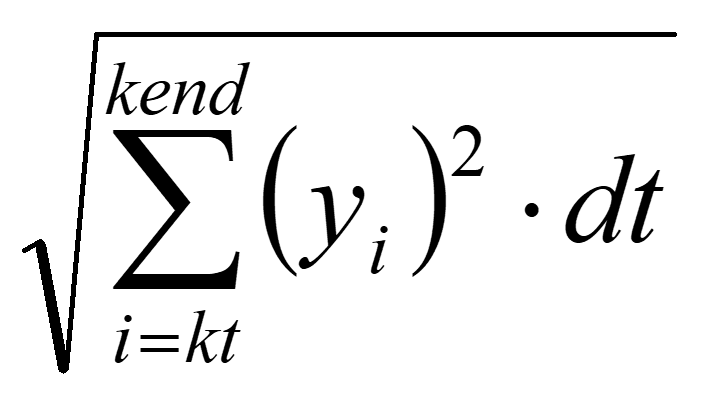
ここで、yiはインデックスiでインパルス応答波形の瞬時値で、ktは時刻tに相当するインデックスで、kendは最終インデックスです。またdtは時間刻みです。
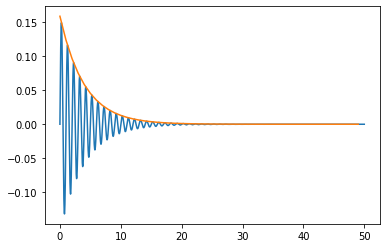
以上をコードにしたのが図4で、これを動作させると、図5に示すように、インパルス波形を青色の曲線で、また、減衰曲線を橙色の曲線で表示します。図を見ると、橙色の減衰曲線はインパルス応答波形の極大値を通過していることがわかります。つまり、得られた減衰曲線の自然対数を求めて、最小二乗法により、その傾きδを求めます。具体的には、numpy.polyfit(x,y,1)とすると、xとyの1次回帰式の係数を[傾き、y切片]の配列で返します。次に、下記の式から、減衰比ζは傾きδを固有角周波数ωnで割ったものになります。
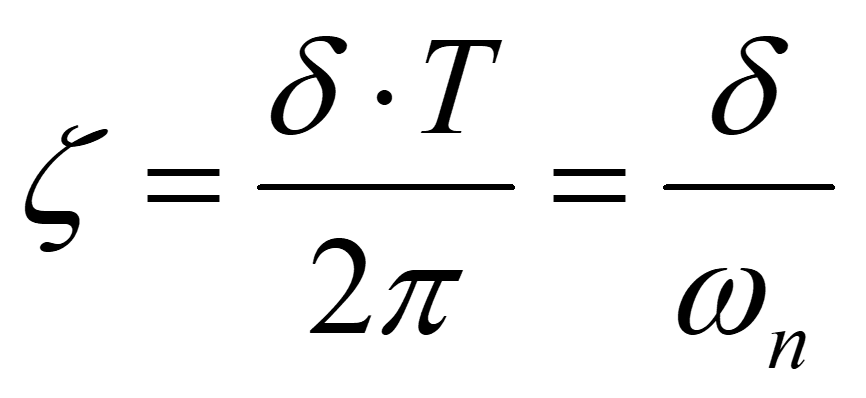

プログラムコード全体と動作結果
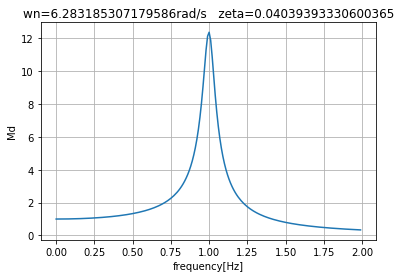
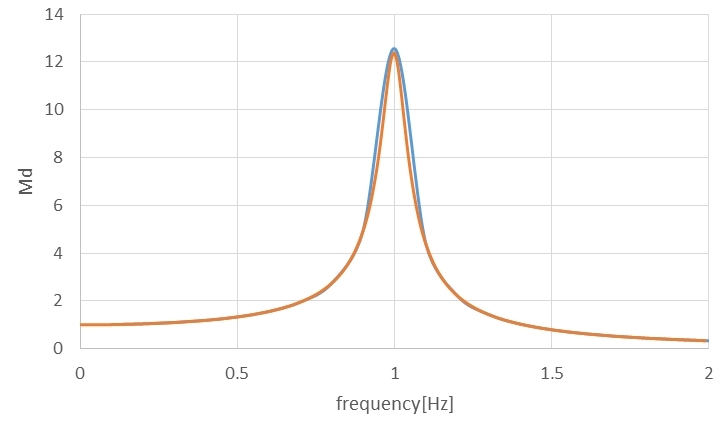
以上をまとめると、図6に示すコードとなります。図6のコードを動作させると、図7に示す振幅倍率の周波数特性をプロットし、その結果をMd.csvというcsvファイルとして出力します。Md.csvファイルを表計算ソフト等で開き、振幅倍率をプロットすると、図8の橙色の曲線となります。図中青色の曲線は、いきなりOpenFOAM第62回で説明の、隣り合った極大値同士から計算した結果です。図を見ると、ほとんど同じ結果となることがわかります。

今回は、インパルス応答解析の自動化というテーマで、主にプログラムコードについて説明しました。
次回は、いきなりOpenFOAM第63回で説明したスロッシングの解析結果から振幅倍率を求めてみます。
このページでは、各アプリケーションの操作説明は省略しています。FreeCADの具体的な操作については、いきなりOpenFOAM第5回および第7回、OpenFOAMでの計算実行は第8回、ParaViewの操作については第3回、第4回および第8回を参考にしてみてください。
おことわり
本コンテンツの動作や表示はお使いのバージョンにより異なる場合があります。
本コンテンツの動作ならびに設定項目等に関する個別の情報提供およびサポートはできかねますので、あらかじめご了承ください。
本コンテンツは動作および結果の保証をするものではありません。ご利用に際してはご自身の判断でお使いいただきますよう、お願いいたします。

