CFD解析結果を用いたサロゲートモデルの構築
サロゲート(代理)モデルとは、CFD解析のように計算コストの高いシミュレーション結果を、近似関数として簡略化する手法です。これにより、即座に結果が得られるため、迅速な判断が求められる設計現場で広く活用されています。
今回は、そり率と傾き角が異なるドローン用プロペラに対してCFD解析を行い、その解析結果からサロゲートモデルを構築した事例を紹介します。
サロゲートモデルの概要
サロゲートモデルは、図1に示すように、設計変数(今回は「そり率」と「傾き角」)を入力とし、目的変数(「推進力」と「トルク」)を出力する関数です。モデル単体では正しい出力が得られないため、事前に設計変数とそれに対応する実験またはCAE解析結果を用いて学習させる必要があります。

図2はモデル構築の流れを示しています。まず、「実験計画法」により目的変数を精度良く予測できるような設計変数の組み合わせを決定します。代表的な手法としてラテン超格子法があり、今回はこの方法により12通りの組み合わせを生成しました。

実験計画と設計変数の設定
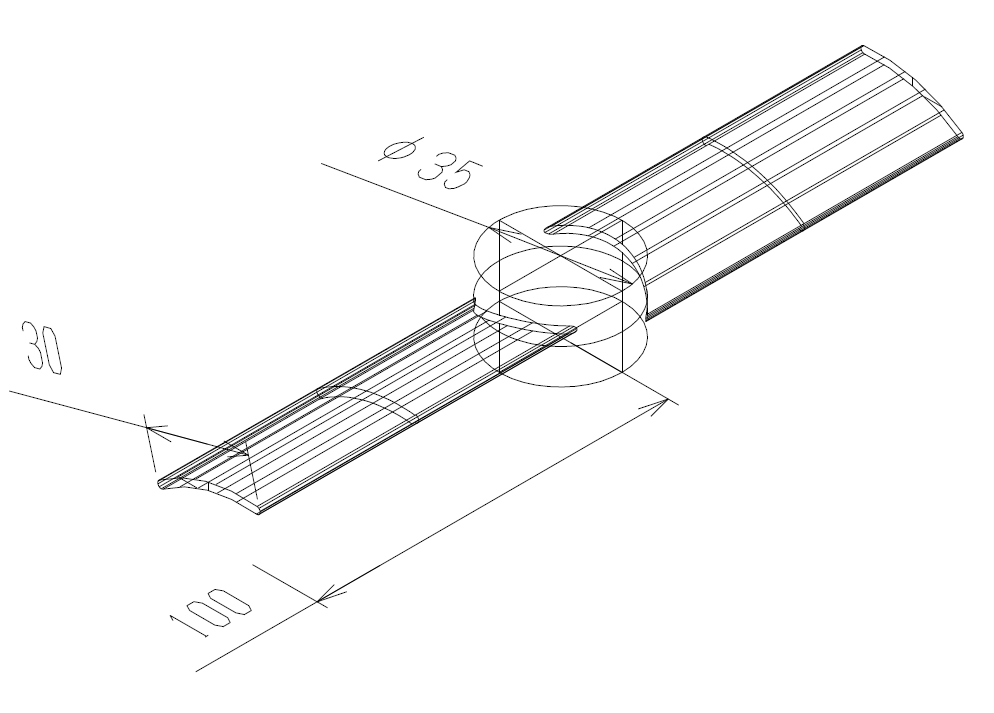
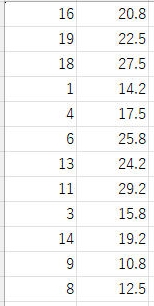
図3に示すプロペラをベースの形状とし、そり率が0〜20%、傾き角が10〜30度の範囲で設計できるものとします。図4には、実験計画法の1つである、ラテン超格子法により求めた、12通りのそり率と傾き角の組み合わせを示しています。
CFD解析の実施
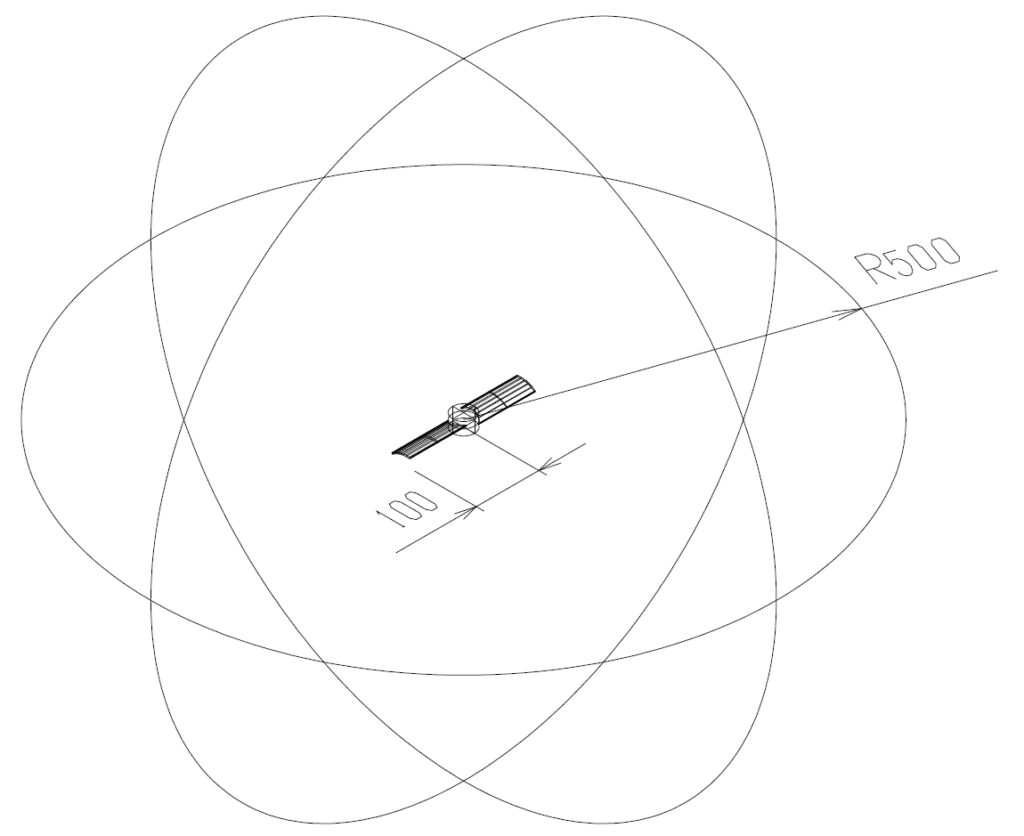
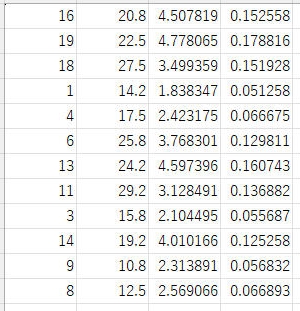
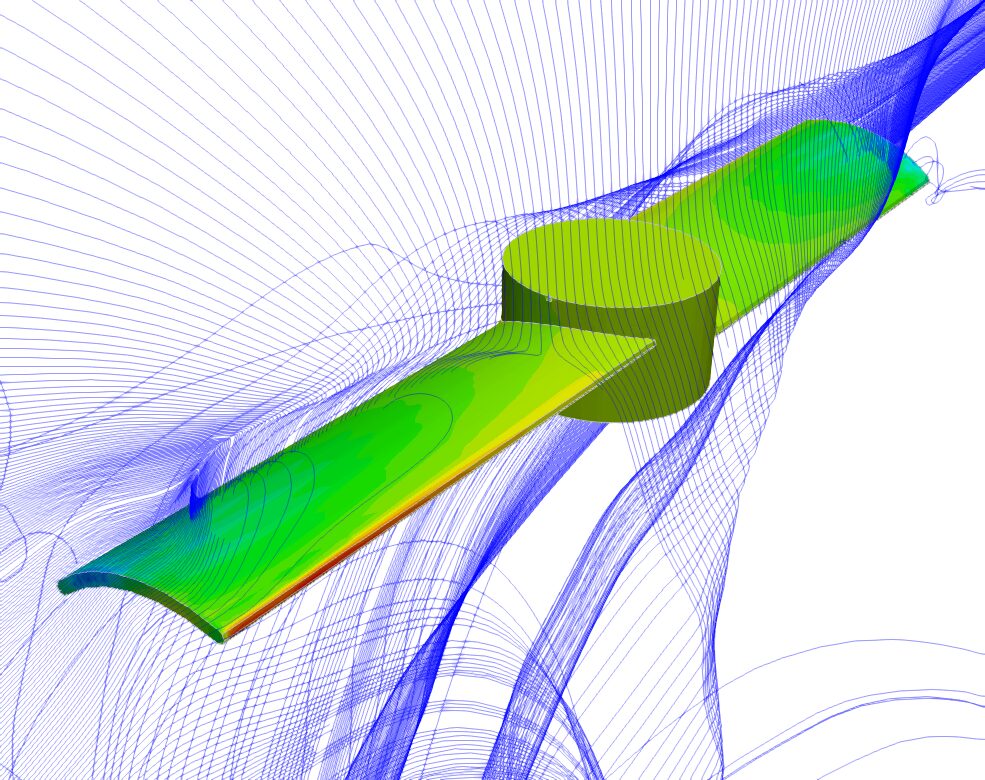
図5に示すCFD解析モデルを用いて、12通りの設計変数で計算を行い、図6に示す、各組み合わせの推進力とトルクを算出します。
サロゲートモデルの構築
12通りのCFD解析結果から、設計変数と対応する目的変数を学習させます。
モデル化の細かい説明は割愛しますが、サロゲートモデルの構築が完了すると、CFDで計算した条件以外の任意の設計変数に対する目的変数(推力とトルク)を算出することが可能となります。
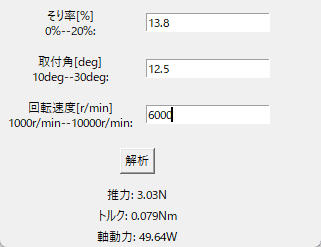
構築したサロゲートモデルを、図7のようなGUIアプリケーションにすることで、誰でも設計変数(そり率・傾き角・回転速度)を入力すれば推進力とトルクを即座に推定することができるようになります。また、表計算ソフトからサロゲートモデルを動作させることもできます。
応答曲面と最適設計
実際の設計では、できるだけ効率の良いプロペラになるようにそり率や傾き角を決めたいのですが、上記のGUIでは1組の設計変数に対する結果(推力とトルク)が分かるだけで、その値が最適(もしくは高効率)なのかを判断することができません。
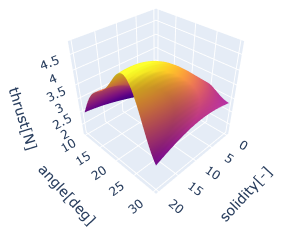
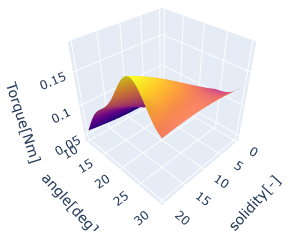
そこで、設計変数を格子状に並べてモデルに入力すると、推進力およびトルクの応答曲面が得られます。図8と図9はそれぞれ、そり率(solidity)と傾き角(angle)に対する推進力とトルクの応答曲面を示しています。両者は類似した傾向を持ち、推進力の増加に伴ってトルクも増加するトレードオフ関係にあることがわかります。
しかしながら、一部には推進力が大きく、トルクが小さい領域も存在しており、この領域の設計変数を選択することで、より効率的なプロペラの設計が可能となります。
サロゲートモデルの精度と活用
最後に、近似式であるサロゲートモデルとCFD解析結果の誤差を検証してみます。
表1は、任意の設計変数に対するサロゲートモデルの出力とCFD解析の結果比較表です。推進力については誤差が0.7%と高い精度で一致している一方、トルクは誤差が15%と少し大きくなっています。この部分に限らず、設計変数の範囲を絞ることや、サンプル数を増やすことで、サロゲートモデルの精度向上が期待できます。
表1 サロゲートモデルでの推定結果とCFD解析結果との比較
| そり率 | 傾き角 | 推進力 | トルク | |
| サロゲートモデル | 13.8 % | 12.5 度 | 3.03 N | 0.079 Nm |
| CFD解析結果 | 13.8 % | 12.5 度 | 3.05 N | 0.093 Nm |
サロゲートモデルは厳密な解析値とは異なりますが、傾向の把握や設計案の絞り込みに非常に有効であり、効率的な設計支援手法として活用することができます。
おことわり
今回の検討はある一定の条件下でのシミュレーション結果になります。異なる条件では違った結果や傾向になる場合があります。また、このシミュレーション結果は実現象の再現を保証するものではありません

